CS算法代写 Graph Theory代写 algorithm代写 cs作业代写
488CS420/520: Graph Theory with Applications to CS, Winter 2022 Homework 2 CS算法代写 Homework Policy: 1. Students should work on homework assignments in groups of preferably three people. Eac...
View detailsSearch the whole station
图论代写 This assignment forms 5% of the assessment for this module. The assignment will be marked out of 20 marks. Please answer all questions,
This assignment forms 5% of the assessment for this module.
The assignment will be marked out of 20 marks.
Please answer all questions, fully justifying your answers. Think about your mathematical style – the aim is for clear, streamlined solutions. Good choice of notation can help clarify your arguments. You may cite results from the notes without proof.
• for each edge e of G, create a vertex ve of G’ ;
• two vertices ve1 , ve2 of V (G’ ) are joined by an edge in G’ if and only if the corresponding edges e1, e2 of E(G) share an endpoint in G.
In other words, G’ has vertices in one-to-one correspondence with the edges of G, and two vertices are adjacent in G’ precisely if the corresponding edges are adjacent in G. For example,
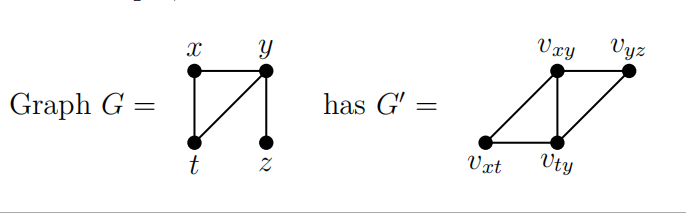

(i) Let Pn denote the path on n vertices (n ≥ 2). Prove that P’n is isomorphic to Pn−1.
(ii) There exists an infinite family of graphs Gn (n ≥ 2) such that
G’n ≌ Kn−1
where Kn−1 is the complete graph on n − 1 vertices.
Give the vertex set and edge set of such a family, and prove that it has the stated property. (4 marks)
Let G be a graph.
(i) Prove that if G is connected then G’ is connected.
(ii) If G’ is connected, is G necessarily connected? Prove or give a counterexample. (5 marks)
Let G be a graph. Write down a formula expressing the degree of a vertex vxy ∈ V (G’ ), in terms of the degree of x, y ∈ V (G). (2 marks)
Prove that if a graph G is Eulerian, then G’ is Eulerian. (2 marks)
Is it true that if a graph G is connected and G’ is Eulerian, then G is Eulerian? Prove or give a counterexample. (2 marks)
Let G be a graph on n vertices {1, . . . , n}, where deg i = di . Prove that
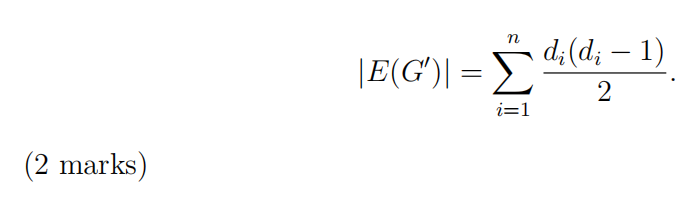

更多代写:Python网课托管推荐 GMAT代考 英国数量分析代上网课 商科essay论文 商业论文写作方法指导 代写EMBA论文
CS420/520: Graph Theory with Applications to CS, Winter 2022 Homework 2 CS算法代写 Homework Policy: 1. Students should work on homework assignments in groups of preferably three people. Eac...
View detailsFall 2021 应用数学计算代写 Read these instructions carefully!!! This project involves predicting what happens to a mortgage loans that have been purchased by FNMA during the Read these instr...
View detailsMath 541 HW1 - Linear Algebra Refresher 数学线性代数代写 Remarks: A) Definition is just a definition, there is no need to justify or explain it. B) Answers to questions with proofs should b...
View detailsDiscrete Mathematics and Graph Theory 离散数学与图论代写 Practice Class 4 1. Give recursive definitions of the following sequences. (a) The sequence of powers of 2: 20 = 1, and for n ≥ 1, _ ...
View details