数学代码代写 MT4512代写 自动机、语言和复杂性代写
597MT4512 Automata, Languages and Complexity 数学代码代写 EXAM DURATION: 2 hours EXAM INSTRUCTIONS: Attempt ALL questions. The number in square brackets shows the maximum marks obtainable for tha...
View detailsSearch the whole station
离散数学与图论代写 Practice Class 4 1. Give recursive definitions of the following sequences. (a) The sequence of powers of 2: 20 = 1, and for n ≥ 1, _
1. Give recursive definitions of the following sequences.
(a) The sequence of powers of 2: 20 = 1, and for n ≥ 1, _______
(b) The Catalan numbers: c0 = 1, and for n ≥ 1, _______

What is the correct order of the lines?
3. Consider the sequence defined by a0 = 0, an = an−1 + 2n for n ≥ 1.
(a) Unravelling gives the non-closed formula _______
(b) Summing the arithmetic progression gives the closed formula _______
(c) Check that the formula in the previous part satisfies the recurrence relation: _______
4. Consider the recurrence relation an = an−1 + 6an−2, for n ≥ 2.
(a) What is the characteristic polynomial?
(b) What are the roots of this polynomial? 离散数学与图论代写
(c) Write down the general solution: _______
(d) Find the solution when a0 = 1, a1 = −1:_______
5. Consider the recurrence relation an = −2an−1 − an−2, for n ≥ 2.
(a) What is the characteristic polynomial?
(b) What are the roots of this polynomial?
(c) Write down the general solution: _______
(d) Find the solution when a0 = 1, a1 = −3: _______
6. Consider the recurrence relation an = −an−2, for n ≥ 2.
(a) What is the characteristic polynomial?
(b) What are the roots of this polynomial?
(c) Write down the general solution: _______
(d) If a0 = 0 and a1 = 1, what is a7?

1. Consider the recurrence relation an = 4an−1 − 4an−2 + 3n + 2, for n ≥ 2.
(a) If pn is a particular solution of this recurrence, the general solution is _______ where bn is a general solution of the homogeneous recurrence relation, i.e.
bn = 4bn−1 − 4bn−2.
(b) The characteristic polynomial of the homogeneous recurrence is x2 − 4x + 4.
Hence _______
(c) A particular solution of the form pn = An + B is _______
(d) Find the solution of the original recurrence when a0 = 15, a1 = 21: _______
2. Write down the general solution of each of the following recurrence relations, by finding a particular solution of the stated form.
(a) an = 3an−1 + 2 for n ≥ 1; pn = A.
(b) an = 2an−1 + n + 1 for n ≥ 1; pn = An + B.
(c) an = 3an−1 − 2n for n ≥ 1; pn = A2n.
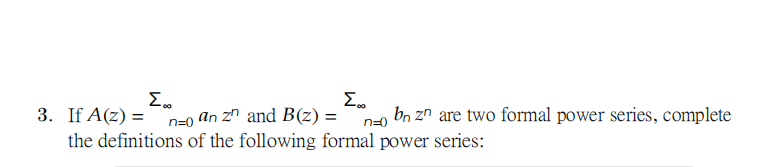
4.For each of the sequences (a)–(g), write the number (i)–(vii) of its generating function.
(a) 1, 2, 22 , 23 , · · · _______
(b) 1, 1, 1, 1, · · · _______
(c) 3, 2, 1, 0, 0, 0, · · · _______
(d) 1, 2, 3, 4, 5, · · · _______
(e) 0, 1, 2, 3, 4, · · · _______
(f) 0, 0, 1, 2, 3, 4, · · · _______
(g) 2, 3, 4, 5, 6, · · · _______

更多代写:计算机科学与技术论文 gmat代考价格 英国会计代上网课 建筑设计Essay代写 加拿大作业代做推荐 留学生考试作弊
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
MT4512 Automata, Languages and Complexity 数学代码代写 EXAM DURATION: 2 hours EXAM INSTRUCTIONS: Attempt ALL questions. The number in square brackets shows the maximum marks obtainable for tha...
View detailsMth 440/540 Homework 计算数论作业代写 (1) Part I a.) Use Mathematica to determine the 100th prime, the 1000th prime, and the 10,000th prime. b.) Use Mathematica to determine the prime (1) ...
View detailsSchool of Computer Science and Technology Discrete Mathematics Examination (A) 离散数学期末代写 1. Single-Choice Questions (2×10=20 points). (1) Among the following four choices, which one ...
View detailsMath 541 HW1 - Linear Algebra Refresher 数学线性代数代写 Remarks: A) Definition is just a definition, there is no need to justify or explain it. B) Answers to questions with proofs should b...
View details