数学复数分析代写 MATH 132代写 复数分析代考 数学代考

MATH 132: Complex Analysis

Final Exam

数学复数分析代写 This is a take-home exam. The following rules regarding the take-home format apply: • The exam is an open-book/open-notes/open-internet exam.

This is a take-home exam. The following rules regarding the take-home format apply:

• The exam is an open-book/open-notes/open-internet exam.

You cannot collaborate in any way with any individual on the exam. Any form of communication/consultation/collaboration with another person about the exam is expressly prohibited— this includes, but is not limited to, Zoom meetings, email, telephone calls, texting, making posts on stack exchanges, etc. Violation of the no-collaboration policy is a violation of the UCLA code of student conduct and will come with serious consequences.

• The instructor reserves the right to ask any student for clarification regarding any of the student’s exam answers at any time during a two week period after the day of the exam. This may require a Zoom meeting with the instructor.

You are required to show your work on each problem of this exam. The following rules apply: 数学复数分析代写

• All answers must be justified. Mysterious or unsupported answers will not receive credit. A correct answer, unsupported by calculations and/or explanation will receive no credit; an incorrect answer supported by substantially correct calculations and explanations might still receive partial credit.

• Although you may use a calculator, it is not necessary. If you do use one, you still need to show your work and justify the computation, as you would on a test without calculators.

Be aware that calculators often produce rational approximations to numerical answers rather than the precisely correct answer, e.g., π ≠ 3.14.

• If you use a theorem or proposition from class or the notes or the textbook or a result established in the homework, you must indicate this and explain why the theorem may be applied.

• Organize your work, in a reasonably neat and coherent way, in the space provided. Work scattered all over the page without a clear ordering will receive very little credit.

Good luck!

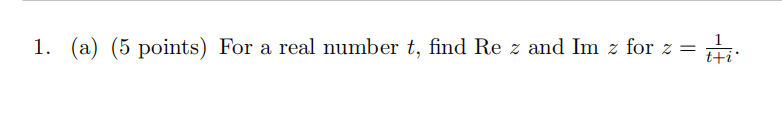
(b) (5 points) For a real number a > 0, express w = a − ai in polar coordinates, re^iθ .

2. (10 points) Consider a function of the form 数学复数分析代写

f(z) = aIm z + ibRe z,

where a and b are real constants. Under what conditions on a and b is the function f(z) entire? Justify your answer.

(b) (8 points) Find a conformal mapping with domain R and whose range is an infinite horizontal strip {z ∈ C : a < Im z < b}. Specify the values of a and b and justify why the map is conformal.

Hint. It will be helpful to consider a particular branch of log(z − 1).

4. (10 points) 数学复数分析代写

Suppose u is harmonic and that v is a harmonic conjugate for u in D. Show that uv is harmonic in D.

5.

Compute the following integrals using any applicable method. Express your answers in Cartesian coordinates, a + ib.

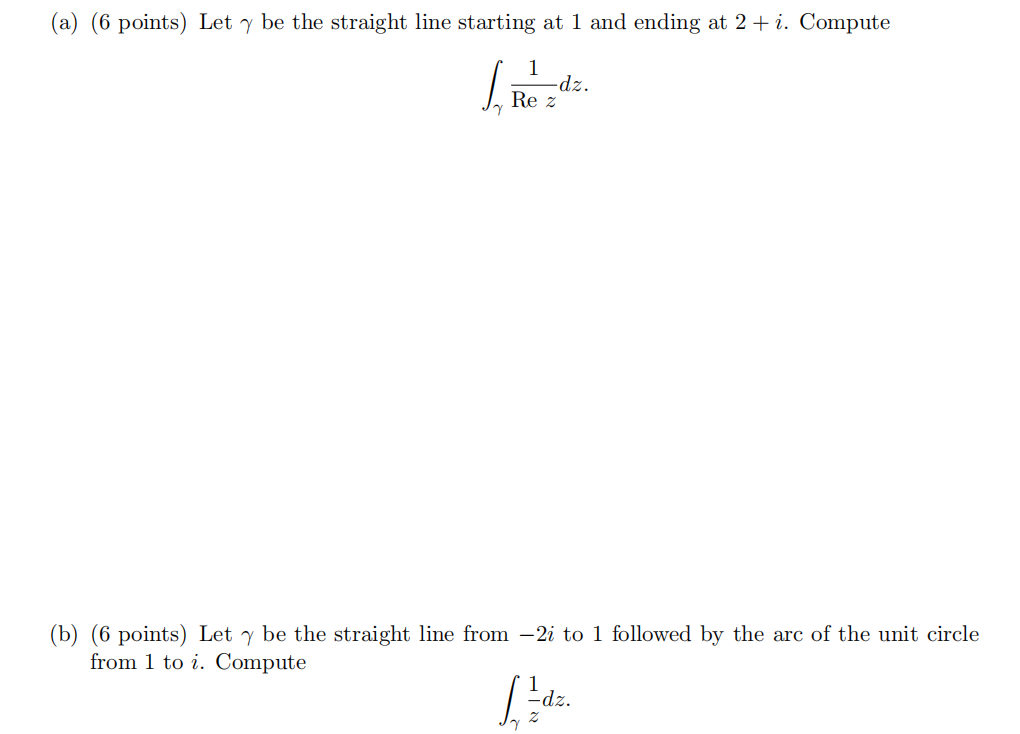
Hint. We have a theorem that makes for a simpler computation than using the definition of line integral.

7. Consider the function

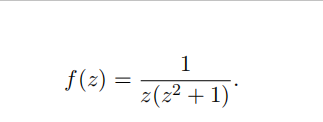
(a) (6 points) Find the Laurent series expansion of f(z) which is centered at 0 and converges at z = 1/2.

(b) (6 points) Find the Laurent series expansion of f(z) which is centered at 0 and converges at z = 2.

9. (10 points) 数学复数分析代写

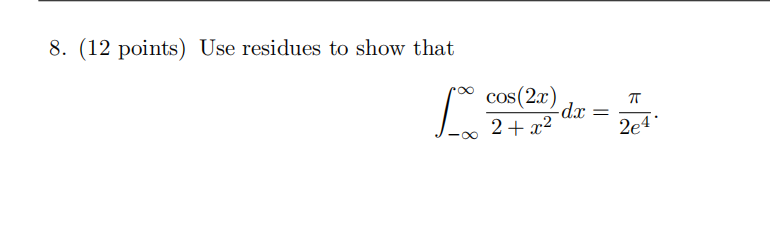
Circle each question as True or False. You do not have to justify your answers.

(a) T / F : If |z| < 1, then the point on the sphere which stereographically projects to z has the form (X, Y, Z) with Z < 0.

(b) T / F : If f(z) is real-valued and entire, then f is constant.

(c) T / F : The multivalued function (z + 1)^1/4 (z − 1)^3/4 has a continuous branch defined on the domain C \ [−1, 1].

(d) T / F : Any fractional linear transformation f(z) maps straight lines in its domain to other straight lines.

(e) T / F : If u(x, y) is harmonic on a domain D, then u has a harmonic conjugate on D.

(f) T / F : There is an entire function whose range is all complex numbers in the open unit disk.

(g) T / F : If z₀ is an removable isolated singularity of f(z), then Res[f, z₀] = 0.

(j) T / F : If f(z) has a pole of order N > 1 at z₀, then (z − z₀)f(z) has a pole of order N − 1 > 0.

更多代写：C#Online Test代写  线上考试作弊方法  英国law法律学作业代写  essay作业代写机构式  research写作方法 数学期末考试练习代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写